
‘ a + 6 = 9’ and ‘2 a + 3 = 9’ are equivalent since they both have the single root ‘ a = 3’.Īn equation of the form ‘ ax + b = 0’ where a ≠ 0 is an equation of the first degree in the unknown x, or simple linear equation If two equations have the same root, they are called equivalent equations, e.g. Instructional Note: Connect to physical situations, e.g., finding the perimeter of a square of area 2. Sometimes the symbol ≡ (equivalent) is used to distinguish an identity from a conditional equation Explain why sums and products of rational numbers are rational, that the sum of a rational number and an irrational number is irrational and that the product of a nonzero rational number and an irrational number is irrational.

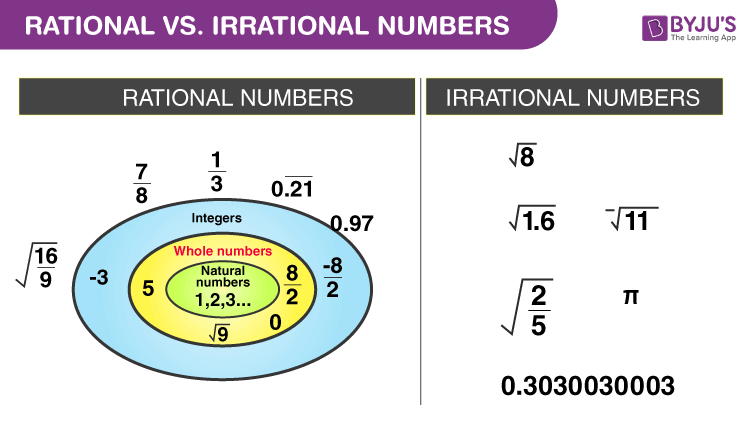
In an identity both terms (= sides) are equal for all values of the unknown number (or numbers), e.g. There's actually an infinite number of rational and an infinite number of irrational numbers. And the size of these circles don't show how large these sets are. In maths two kinds of equations are differed: conditional equations ( = equations) and identical equations ( = identities). And if something cannot be represented as a fraction of two integers, we call irrational numbers. This value is called the root or the solutionof the equation. To solve an equation means to find the numerical value of the letter which fits the equation. The letter ‘ a’ stands for an unknown (number or quantity). For example, ‘ a + 4 = 6’ is an equation stating that ‘ a + 4’ equals ‘6’. Use information from the text.Įquation is an algebraic expression to state equality of two numbers or quantities. Give your own examples of primes, rational and irrational numbers. Define which of the numbers are a/ primes, b/ rational numbers, c/ irrational numbers:ĥ,5 13 0,666… 0 59 e 7,125 -9,02 19 0,3131. What is a rational number? Irrational number? Example of irrational numbers:, , π.Ī surd is a root of rational number which cannot be expressed as rational number, e.g. These are square roots of non-square numbers, cube roots of non-cube numbers, the number π and surds.
Irrational numbers cannot be written as a fraction. Examples of rational numbers: 3 -2 0,1 4,(3) 6. The number is rational if it can be written in the form where b ≠ 0 and ‘ a’ and ‘ b’ are integers. For example, 16 = 2 × 2 × 2 × 2 17 is a prime 44 = 11 × 2 × 2 53 is a prime.Īll real numbers are rational or irrational. The number 1 has only one factor that’s why it is not a prime.Įvery natural number bigger than 1 is either a prime or can be written as a product of primes. For example, the numbers 5, 37, 111, 1093 can be divided only by 1 and themselves. There are numbers having exactly two factors, 1 and the number itself.


 0 kommentar(er)
0 kommentar(er)
